Giải hệ phương trình, phương trình bằng máy tính Casio fx-580VN X

Phương thức Equation / Func được cho phép tất cả chúng ta

Giải hệ phương trình hai ẩn, ba ẩn và bốn ẩn
Giải phương trình bậc hai, bậc ba và bậc bốn
Tìm cực trị của hàm số bậc hai, bậc ba
Gán giá trị của nghiệm, cực trị vào các biến nhớ

Ngoài ra Casio fx-580VN X còn được cho phép tất cả chúng ta thiết lập có hiển thị nghiệm phức khi giải phương trình hay không

1 Giải hệ phương trình

Giải hệ phương trình $\left\{\begin{array}{ll}2x+y&=4\-2x+y&=0 \end{array}\right.$

Bước 1 Nhấn phím MENU

Bạn đang đọc: Giải hệ phương trình, phương trình bằng máy tính Casio fx-580VN X

Bước 2 Nhấn phím 9 để chọn phương thức Equation/Func

Bước 3 Chọn Simul Equation để giải hệ phương trình

Bước 4 Nhập số ẩn của hệ phương trình

Ở đây hệ phương trình cần giải có hai ẩn nên mình sẽ nhấn phím 2

Bước 5 Nhập hệ số thứ nhất => nhấn phím = => … => nhập hệ số cuối cùng => nhấn phím =

Bước 6 Nhấn phím =

Bước 7 Nhấn phím =

Vậy nghiệm của hệ phương trình đã cho là $(1, 2)$

Chú ý 1Một số hệ phương trình khi giải sẽ thu được nghiệm đặc biệt quan trọng

All Real Numbers hệ phương trình đã cho có vô số nghiệm
No Solution hệ phương trình đã cho vô nghiệm

2 Giải phương trình

Giải phương trình $x^2-3x+2=0$

Bước 1 Nhấn phím MENU

Bước 2 Nhấn phím 9 để chọn phương thức Equation/Func

Bước 3 Chọn Polynomial để giải phương trình

Bước 4 Chọn bậc của phương trình

Ở đây mình cần giải phương trình bậc hai nên nhấn phím 2

Bước 5 Nhập thông số thứ nhất => nhấn phím = => … => nhập thông số sau cuối => nhấn phím =

Bước 6 Nhấn phím =

Bước 7 Nhấn phím =

Vậy nghiệm của phương trình đã cho là $\{2,1\}$

Ngoài ra nếu tiếp tục nhấn phím = chúng ta sẽ tìm được tọa độ điểm cực tiểu của hàm số $\left(\dfrac{3}{2}, -\dfrac{1}{4}\right)$

3 Ứng dụng

Trong thực tiễn không phải khi nào tất cả chúng ta cũng gặp trực tiếp bài toán “ Giải hệ phương trình … ”, “ Giải phương trình … ”
Nhiều bài toán khi triển khai các phép biến hóa sơ cấp sẽ dẫn tới việc giải hệ phương trình, phương trình tương ứng

Một số bài toán thường gặp

Xem thêm: [CẦN BIẾT] Uống gì để giải rượu bia nhanh nhất? Ăn gì để giải rượu nhanh: canh, cháo, quả …? | Omi Pharma

Viết phương trình đường thẳng đi qua 2 điểm
Viết phương trình Parabol đi qua 3 điểm
Viết phương trình đường tròn đi qua 3 điểm
Viết phương trình mặt cầu đi qua 4 điểm
Viết phương trình đường thẳng đi qua 2 điểm cực trị của hàm số bậc 3
Tính khoảng cách giữa 2 điểm cực trị của hàm số bậc 3
…

3.1 Viết phương trình mặt cầu đi qua 4 điểm

Viết phương trình mặt cầu đi qua 4 điểm

Giả sử phương trình mặt cầu cần tìm có dạng $x^2+y^2+z^2-2ax-2by-2cz+d=0$ và tọa độ 4 điểm đi qua là $(x_1, y_1, z_1)$ , $(x_2, y_2, z_2)$ , $(x_3, y_3, z_3)$ và $(x_4, y_4, z_4)$

Khi đó $(a, b, c ,d)$ là nghiệm của hệ phương trình $\left\{\begin{array}{llll}-2ax_1-2by_1-2cz_1+d=-(x_1^2+y_1^2+z_1^2)\-2ax_2-2by_2-2cz_2+d=-(x_2^2+y_2^2+z_2^2)\-2ax_3-2by_3-2cz_3+d=-(x_3^2+y_3^2+z_3^2)\-2ax_4-2by_4-2cz_4+d=-(x_4^2+y_4^2+z_4^2)\end{array}\right.$

Viết phương trình mặt cầu đi qua $A(2, 4, -1), B(1, 4, -1), C(2, 3, 4), D(2, 2, -1)$

Bước 1 Nhập hệ phương trình

Bước 2 Nhấn phím =

Vậy phương trình mặt cầu cần tìm là $x^2+y^2+z^2-3x-6y-\dfrac{14}{5}z+\dfrac{31}{5}=0$

3.2 Cực trị của hàm số bậc ba

Cực trị của hàm số bậc ba

Cho hàm số bậc ba $ax^3+bx^2+cx +d$

Cực trị của hàm số bậc ba

Giải phương trình bậc ba tương ứng

Phương trình đường thẳng đi qua hai điểm cực trị

Giả sử phương trình đường thẳng cần tìm có dạng 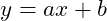$y=ax+b$ và tọa độ của 2 điểm cực trị là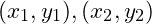 $(x_1, y_1), (x_2, y_2)$
Khi đó 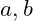$a, b$ là nghiệm của hệ phương trình $\left\{\begin{array}{ll}ax_1+b&=y_1\ax_2+b&=y_2\end{array}\right.$

Khoảng cách giữa hai điểm cực trị

Giả sử tọa độ của 2 điểm cực trị là
Khi đó khoảng cách giữa hai điểm cực trị sẽ được tính theo công thức $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

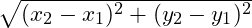
Chú ý 3.2

Nếu phương trình đường thẳng cần tìm trùng hoặc song song với trục tung thì phương pháp này không khả dụng
Vì hoành độ và trung độ của các điểm cực trị thường “xấu” nên ta nên gán chúng vào các biến nhớ

Cho hàm số bậc ba $x^3 - 6 x^2 + 11 x - 6$

a ) Tìm 2 điểm cực trị của hàm số
b ) Viết phương trình đường thẳng đi qua 2 điểm cực trị
c ) Tính khoảng cách giữa hai điểm cực trị

Bước 1 Nhập phương trình

Bước 2 Nhấn phím =

Vậy hai điểm cực trị của hàm số đã cho là $\left(\dfrac{6-\sqrt{3}}{3}, \dfrac{2 \sqrt{3}}{9}\right)$ và $\left(\dfrac{6+\sqrt{3}}{3},-\dfrac{2 \sqrt{3}}{9}\right)$