Tìm nghiệm của phương trình bằng tính năng SOLVE

advietsofavn
Estimated read time 8 min read

Tính năng SOLVE cho phép chúng ta tìm nghiệm của một phương trình bất kì bằng cách sử dụng phương pháp Newton

Tuy tính năng SOLVE trên Casio fx-580VN X tương tự như như trên Casio fx-570VN Plus nhưng vẫn có 2 điểm độc lạ

  • Quá trình giải phương trình nhanh hơn do máy có cấu hình mạnh hơn
  • fx-580VN X có thể SOLVE với mọi biến nhớ trong khi fx-570VN Plus chỉ có thể SOLVE với biến x

1 Lưu ý

  • Tính năng SOLVE chỉ có thể giải được phương trình một biến vì vậy khi gặp phương trình nhiều biến máy tính vẫn giải theo một biến. Giải biến nào là do bạn chỉ định và các biến còn lại được xem như các hằng số
  • Phương trình có nhiều nghiệm thì máy tính chỉ tìm ra một nghiệm. Tìm ra nghiệm nào phụ thuộc vào giá trị x ban đầu
  • Một số trường hợp khi gặp các phương trình phức tạp máy sẽ thông báo Continue: [=] hỏi bạn có muốn tiếp tục tìm nghiệm không. Nhấn phím = để tiếp tục, nhấn phím AC để dừng
  • Đối với các phương trình quá phức tạp máy tính có thể không tìm được nghiệm cho dù nghiệm tồn tại

2 Ví dụ minh họa

Dấu bằng trong phương trình là dấu bằng màu đỏ chứ không phải dấu bằng màu đen mà chúng ta vẫn thường sử dụng

Ví dụ 2.1

Giải phương trình 2x-3=4

Bước 1 Nhập phương trình vào máy tính

Bước 2 Nhấn phím SOLVE

Bước 3 Nhập giá trị x ban đầu, thông thường bạn cứ nhập là 0

Bước 4 Nhấn phím =

Bước 5 Nhấn phím =


Quan sát màn hình hiển thị hiển thị ta nhận thấy

  • là phương trình
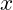  • x là biến
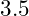  • 3.5 là nghiệm
  • L-R có nghĩa là vế trái – vế phải. Giá trị này bằng thì nghiệm tìm được là nghiệm chính xác hoặc là nghiệm gần đúng

Vậy phương trình đã cho có nghiệm là hay \dfrac{7}{2}

Nghiệm tìm được bằng tính năng này sẽ hiển thị dưới dạng thập phân. Nếu muốn hiển thị dưới dạng phân số, căn thức (không phải nghiệm nào cũng hiển thị được dưới hai dạng này) bạn hãy nhấn phím Ans => nhấn phím =

Ví dụ 2.2

Giải phương trình x^5 - 15 x^4 + 85 x^3 - 225 x^2 + 274 x = 120

Phương trình đã cho năng lực có nhiều nghiệm, nếu chỉ sử dụng tính năng SOLVE thì không hề tìm được các nghiệm còn lại
Có nhiều thủ pháp giúp xử lý yếu tố này, thủ pháp được trình diễn bên dưới dưới là một trong các thủ pháp được sử dụng nhiều nhất

Bước 1 Thực hiện các phép biến đổi sơ cấp đưa phương trình về dạng f(x)=0

x^5 - 15 x^4 + 85 x^3 - 225 x^2 + 274 x - 120 = 0

Bước 2 Nhập f(x) vào máy tính

Bước 3 Nhấn phím = để lưu f(x)


Chú ý 2

Giá trị hiển thị trên màn hình của bạn có thể không phải -120, là bao nhiêu phụ thuộc vào giá trị của biến x

Bước 4 Tiến hành SOLVE để tìm nghiệm

Vậy nghiệm thứ nhất là 1

Bước 5 Giả sử x_1 là nghiệm thứ nhất, để tìm nghiệm thứ nhì chúng ta nhập (f(x)) \div (x-x_1)

Ở đây vì f(x) đã được máy tính lưu lại nên chúng ta chỉ cần nhấn phím  rồi chỉnh sửa lại là xong

Bước 6 Tiến hành SOLVE để tìm nghiệm

Vậy nghiệm thứ nhì là 2

Bước 7 Giả sử x_2 là nghiệm thứ nhì để tìm nghiệm thứ ba chúng ta nhập (f(x)) \div (x-x_1) \div (x-x_2)

Bước 8 Tiến hành SOLVE để tìm nghiệm

Vậy nghiệm thứ ba là 3

Bước 9 Thực hiện tương tự như Bước 5, Bước 6 để tìm tất cả các nghiệm còn lại nếu có

Quy trình sẽ dừng lại khi máy tính hiển thị Cannot Solve tức phương trình đã hết nghiệm

Vậy tập nghiệm của phương trình đã cho là \{1, 2, 3, 4, 5\}

Ví dụ 2.3

Giải phương trình ax+b=0 trong trường hợp a=2, b=3 và a=7, b=11

Bước 1 Nhập phương trình vào máy tính

Bước 2 Nhấn phím SOLVE

Bước 3 Máy hỏi A= bao nhiêu, nhấn phím

Bước 4 Nhấn phím =


Bước 5 Vì là biến chạy nên tất cả chúng ta không cần nhập giá trị cho nó, nếu vẫn muốn bạn hãy nhập

Bước 6 Nhấn phím =

Bước 7 Máy hỏi B= bao nhiêu, nhấn phím

Bước 8 Nhấn phím =

Bước 9 Phương trình vừa nhập có 3 biến nên ta cần chỉ ra biến nào là biến chạy. Ở đây x là biến chạy nên ta sẽ nhấn phím  ,  để chọn

Bước 10 Nhấn phím =

Vậy phương trình trong trường hợp có nghiệm là -1.5

Bước 11 Thực hiện lại các bước trên, bắt đầu từ Bước 2 để tìm nghiệm của phương trình cho trường hợp

Vậy phương trình trong trường hợp có nghiệm là -1.4

3 Phương trình cá biệt

Ví dụ 3

Giải phương trình \sqrt{x^2+2x+3}=x+1

Theo các chỉ dẫn trong bài viết này thì x=10000000 là nghiệm của phương trình

Tuy nhiên nghiệm này là SAI vì phương trình này vô nghiệm, thật vậy

    \[\sqrt{x^2+2x+3}=x+1 \Leftrightarrow \left\{ \begin{array}{ll} x& \geq 0, \forall x \in \mathbb{R}\ 3&=1 \end{array} \right.\]

Khi sử dụng tính năng SOLVE tìm nghiệm của phương trình nếu thu được nghiệm là một số lớn bất thường thì ta nên kiểm tra lại

Không sử dụng tính năng CALC để kiểm tra cho trường hợp này vì tính năng CALC cũng “ ngáo sửu ” với phương trình này
WolframAlpha là lựa chọn số 1

Hãy chia sẽ nếu thấy hữu dụng …

Avatar for advietsofavn
advietsofavn https://vietsofa.vn

You May Also Like

More From Author

+ There are no comments

Add yours