Sách Giải Bài Tập Toán Lớp 8 Bài 4: Phương Trình Tích – Luyện Tập (trang 17)

Xem toàn bộ tài liệu Lớp 8: tại đây

Xem thêm các sách tham khảo liên quan:

Sách giải toán 8 Bài 4 : Phương trình tích – Luyện tập ( trang 17 ) giúp bạn giải các bài tập trong sách giáo khoa toán, học tốt toán 8 sẽ giúp bạn rèn luyện năng lực suy luận hài hòa và hợp lý và hợp logic, hình thành năng lực vận dụng kết thức toán học vào đời sống và vào các môn học khác :

Trả lời câu hỏi Toán 8 Tập 2 Bài 4 trang 15: Phân tích đa thức P(x) = (x^2 – 1) + (x + 1)(x – 2) thành nhân tử.

Lời giải

P ( x ) = ( x ^ 2 – 1 ) + ( x + 1 ) ( x – 2 )
P ( x ) = ( x – 1 ) ( x + 1 ) + ( x + 1 ) ( x – 2 )
P ( x ) = ( x + 1 ) ( x – 1 + x – 2 )
P ( x ) = ( x + 1 ) ( 2 x – 3 )

Trả lời câu hỏi Toán 8 Tập 2 Bài 4 trang 15: Hãy nhớ lại một tính chất của phép nhân các số, phát biểu tiếp các khẳng định sau:

Trong một tích nếu có một thừa số bằng 0 thì … ; ngược lại, nếu tích bằng 0 thì tối thiểu một trong các thừa số của tích …
Lời giải
Trong một tích nếu có một thừa số bằng 0 thì tích bằng 0 ; ngược lại, nếu tích bằng 0 thì tối thiểu một trong các thừa số của tích bằng 0

Trả lời câu hỏi Toán 8 Tập 2 Bài 4 trang 16: Giải phương trình:

( x – 1 ) ( x2 + 3 x – 2 ) – ( x3 – 1 ) = 0 .
Lời giải
( x – 1 ) ( x2 + 3 x – 2 ) – ( x3 – 1 ) = 0
⇔ ( x – 1 ) ( x2 + 3 x – 2 ) – ( x – 1 ) ( x2 + x + 1 ) = 0
⇔ ( x – 1 ) [ ( x2 + 3 x – 2 ) – ( x2 + x + 1 ) ] – 0
⇔ ( x – 1 ) ( 2 x – 3 ) = 0
⇔ x – 1 = 0 hoặc 2 – 3 = 0
x – 1 = 0 ⇔ x = 1
2 x – 3 = 0 ⇔ x = 3/2
Vậy tập nghiệm của phương trình là S = { 1 ; 3/2 }

Trả lời câu hỏi Toán 8 Tập 2 Bài 4 trang 17: : Giải phương trình (x3 + x2) + (x2 + x) = 0.

Lời giải
( x3 + x2 ) + ( x2 + x ) = 0
⇔ x2 ( x + 1 ) + x ( x + 1 ) = 0
⇔ ( x2 + x ) ( x + 1 ) = 0
⇔ x ( x + 1 ) ( x + 1 ) = 0
⇔ x = 0 hoặc x + 1 = 0
⇔ x = 0 hoặc x = – 1
Vậy tập nghiệm của phương trình là : S = { 0 ; – 1 }
Bài 4: Phương trình tích

Bài 21 (trang 17 SGK Toán 8 tập 2): Giải các phương trình:

a ) ( 3 x – 2 ) ( 4 x + 5 ) = 0
b ) ( 2,3 x – 6,9 ) ( 0,1 x + 2 ) = 0
c ) ( 4 x + 2 ) ( x2 + 1 ) = 0
d ) ( 2 x + 7 ) ( x – 5 ) ( 5 x + 1 ) = 0
Lời giải:
a ) ( 3 x – 2 ) ( 4 x + 5 ) = 0
⇔ 3 x – 2 = 0 hoặc 4 x + 5 = 0
+ 3x – 2 = 0 ⇔ 3x = 2 ⇔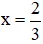

+ 4x + 5 = 0 ⇔ 4x = -5 ⇔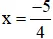

Vậy phương trình có tập nghiệm
b ) ( 2,3 x – 6,9 ). ( 0,1 x + 2 ) = 0
⇔ 2,3 x – 6,9 = 0 hoặc 0,1 x + 2 = 0
+ 2,3 x – 6,9 = 0 ⇔ 2,3 x = 6,9 ⇔ x = 3 .
+ 0,1 x + 2 = 0 ⇔ 0,1 x = – 2 ⇔ x = – 20 .
Vậy phương trình có tập nghiệm

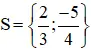
c ) ( 4 x + 2 ) ( x2 + 1 ) = 0
⇔ 4 x + 2 = 0 hoặc x2 + 1 = 0
+ 4x + 2 = 0 ⇔ 4x = -2 ⇔ x =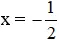
+ x2 + 1 = 0 ⇔ x2 = – 1 ( Phương trình vô nghiệm ) .
Vậy phương trình có tập nghiệm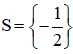
d ) ( 2 x + 7 ) ( x – 5 ) ( 5 x + 1 ) = 0
⇔ 2 x + 7 = 0 hoặc x – 5 = 0 hoặc 5 x + 1 = 0
+ 2 x + 7 = 0 ⇔ 2 x = – 7 ⇔

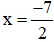
+ x – 5 = 0 ⇔ x = 5 .
+ 5x + 1 = 0 ⇔ 5x = -1 ⇔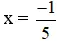

Vậy phương trình có tập nghiệm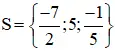

Bài 4: Phương trình tích

Bài 22 (trang 17 SGK Toán 8 tập 2): Bằng cách phân tích vế trái thành nhân tử, giải các phương trình sau:

a ) 2 x ( x – 3 ) + 5 ( x – 3 ) = 0 ;
b ) ( x2 – 4 ) + ( x – 2 ) ( 3 – 2 x ) = 0 ;
c ) x3 – 3×2 + 3 x – 1 = 0 ;
d ) x ( 2 x – 7 ) – 4 x + 14 = 0 ;
e ) ( 2 x – 5 ) 2 – ( x + 2 ) 2 = 0 ;
f ) x2 – x – ( 3 x – 3 ) = 0 .
Lời giải:
a ) 2 x ( x – 3 ) + 5 ( x – 3 ) = 0

⇔ ( 2 x + 5 ) ( x – 3 ) = 0
⇔ 2 x + 5 = 0 hoặc x – 3 = 0
+ 2 x + 5 = 0 ⇔ 2 x = – 5 ⇔ x = – 5/2
+ x – 3 = 0 ⇔ x = 3 .
Vậy phương trình có tập nghiệm

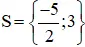
b ) ( x2 – 4 ) + ( x – 2 ) ( 3 – 2 x ) = 0
⇔ ( x – 2 ) ( x + 2 ) + ( x – 2 ) ( 3 – 2 x ) = 0
⇔ ( x – 2 ) [ ( x + 2 ) + ( 3 – 2 x ) ] = 0
⇔ ( x – 2 ) ( 5 – x ) = 0
⇔ x – 2 = 0 hoặc 5 – x = 0
+ x – 2 = 0 ⇔ x = 2
+ 5 – x = 0 ⇔ x = 5 .
Vậy tập nghiệm của phương trình là S = { 2 ; 5 } .
c ) x3 – 3×2 + 3 x – 1 = 0
⇔ ( x – 1 ) 3 = 0 ( Hằng đẳng thức )
⇔ x – 1 = 0
⇔ x = 1 .
Vậy tập nghiệm của phương trình là S = { 1 } .
d ) x ( 2 x – 7 ) – 4 x + 14 = 0
⇔ x ( 2 x – 7 ) – 2 ( 2 x – 7 ) = 0
⇔ ( x – 2 ) ( 2 x – 7 ) = 0
⇔ x – 2 = 0 hoặc 2 x – 7 = 0
+ x – 2 = 0 ⇔ x = 2 .
+ 2 x – 7 = 0 ⇔ 2 x = 7 ⇔ x = 7/2
Vậy tập nghiệm của phương trình là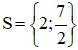
e ) ( 2 x – 5 ) 2 – ( x + 2 ) 2 = 0
⇔ [ ( 2 x – 5 ) + ( x + 2 ) ]. [ ( 2 x – 5 ) – ( x + 2 ) ] = 0
⇔ ( 3 x – 3 ) ( x – 7 ) = 0
⇔ 3 x – 3 = 0 hoặc x – 7 = 0
+ 3 x – 3 = 0 ⇔ 3 x = 3 ⇔ x = 1 .
+ x – 7 = 0 ⇔ x = 7 .
Vậy phương trình có tập nghiệm S = { 1 ; 7 } .
f ) x2 – x – ( 3 x – 3 ) = 0
⇔ x ( x – 1 ) – 3 ( x – 1 ) = 0
⇔ ( x – 3 ) ( x – 1 ) = 0
⇔ x – 3 = 0 hoặc x – 1 = 0
+ x – 3 = 0 ⇔ x = 3
+ x – 1 = 0 ⇔ x = 1 .
Vậy phương trình có tập nghiệm S = { 1 ; 3 } .
Bài 4: Phương trình tích

Luyện tập (trang 17 sgk Toán 8 Tập 2)

Bài 23 (trang 17 SGK Toán 8 tập 2): Giải các phương trình:

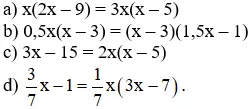
Lời giải:
a ) x ( 2 x – 9 ) = 3 x ( x – 5 )
⇔ x. ( 2 x – 9 ) – x. 3 ( x – 5 ) = 0
⇔ x. [ ( 2 x – 9 ) – 3 ( x – 5 ) ] = 0
⇔ x. ( 2 x – 9 – 3 x + 15 ) = 0
⇔ x. ( 6 – x ) = 0
⇔ x = 0 hoặc 6 – x = 0
+ 6 – x = 0 ⇔ x = 6
Vậy tập nghiệm của phương trình là S = { 0 ; 6 } .
b ) 0,5 x ( x – 3 ) = ( x – 3 ) ( 1,5 x – 1 )
⇔ 0,5 x ( x – 3 ) – ( x – 3 ) ( 1,5 x – 1 ) = 0
⇔ ( x – 3 ). [ 0,5 x – ( 1,5 x – 1 ) ] = 0
⇔ ( x – 3 ) ( 0,5 x – 1,5 x + 1 ) = 0
⇔ ( x – 3 ) ( 1 – x ) = 0
⇔ x – 3 = 0 hoặc 1 – x = 0
+ x – 3 = 0 ⇔ x = 3 .
+ 1 – x = 0 ⇔ x = 1 .
Vậy phương trình có tập nghiệm S = { 1 ; 3 } .
c ) 3 x – 15 = 2 x ( x – 5 )
⇔ ( 3 x – 15 ) – 2 x ( x – 5 ) = 0
⇔ 3 ( x – 5 ) – 2 x ( x – 5 ) = 0
⇔ ( 3 – 2 x ) ( x – 5 ) = 0
⇔ 3 – 2 x = 0 hoặc x – 5 = 0
+ 3 – 2 x = 0 ⇔ 2 x = 3 ⇔ x = 3/2 .
+ x – 5 = 0 ⇔ x = 5 .
Vậy phương trình có tập nghiệm


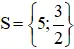
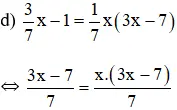
⇔ 3 x – 7 = x ( 3 x – 7 ) ( Nhân cả hai vế với 7 ) .
⇔ ( 3 x – 7 ) – x ( 3 x – 7 ) = 0
⇔ ( 3 x – 7 ) ( 1 – x ) = 0
⇔ 3 x – 7 = 0 hoặc 1 – x = 0
+ 3 x – 7 = 0 ⇔ 3 x = 7 ⇔ x = 7/3 .
+ 1 – x = 0 ⇔ x = 1 .
Vậy phương trình có tập nghiệm

Bài 4: Phương trình tích

Luyện tập (trang 17 sgk Toán 8 Tập 2)

Bài 24 (trang 17 SGK Toán 8 tập 2): Giải các phương trình:

a ) ( x2 – 2 x + 1 ) – 4 = 0
b ) x2 – x = – 2 x + 2
c ) 4×2 + 4 x + 1 = x2 .
d ) x2 – 5 x + 6 = 0 .
Lời giải:
a ) ( x2 – 2 x + 1 ) – 4 = 0

⇔ ( x – 1 ) 2 – 22 = 0
⇔ ( x – 1 – 2 ) ( x – 1 + 2 ) = 0
( Sử dụng hằng đẳng thức )
⇔ ( x – 3 ) ( x + 1 ) = 0
⇔ x – 3 = 0 hoặc x + 1 = 0
+ x – 3 = 0 ⇔ x = 3 .
+ x + 1 = 0 ⇔ x = – 1 .
Vậy tập nghiệm của phương trình là S = { – 1 ; 3 } .
b ) x2 – x = – 2 x + 2
⇔ x2 – x + 2 x – 2 = 0
⇔ x ( x – 1 ) + 2 ( x – 1 ) = 0
⇔ ( x + 2 ) ( x – 1 ) = 0
(Đặt nhân tử chung)

⇔ x + 2 = 0 hoặc x – 1 = 0
+ x + 2 = 0 ⇔ x = – 2
+ x – 1 = 0 ⇔ x = 1 .
Vậy tập nghiệm của phương trình là S = { – 2 ; 1 } .
c ) 4×2 + 4 x + 1 = x2
⇔ 4×2 + 4 x + 1 – x2 = 0
⇔ ( 2 x + 1 ) 2 – x2 = 0
⇔ ( 2 x + 1 – x ) ( 2 x + 1 + x ) = 0
( Sử dụng hằng đẳng thức )
⇔ ( x + 1 ) ( 3 x + 1 ) = 0
⇔ x + 1 = 0 hoặc 3 x + 1 = 0
+ x + 1 = 0 ⇔ x = – 1 .
+ 3 x + 1 = 0 ⇔ 3 x = – 1 ⇔

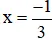
Vậy phương trình có tập nghiệm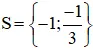
d ) x2 – 5 x + 6 = 0
⇔ x2 – 2 x – 3 x + 6 = 0
( Tách để Open nhân tử chung )
⇔ ( x2 – 2 x ) – ( 3 x – 6 ) = 0
⇔ x ( x – 2 ) – 3 ( x – 2 ) = 0
⇔ ( x – 3 ) ( x – 2 ) = 0
⇔ x – 3 = 0 hoặc x – 2 = 0
+ x – 3 = 0 ⇔ x = 3 .
+ x – 2 = 0 ⇔ x = 2 .
Vậy tập nghiệm của phương trình là S = { 2 ; 3 } .
Bài 4: Phương trình tích

Luyện tập (trang 17 sgk Toán 8 Tập 2)

Bài 25 (trang 17 SGK Toán 8 tập 2): Giải các phương trình:

a ) 2×3 + 6×2 = x2 + 3 x

b ) ( 3 x – 1 ) ( x2 + 2 ) = ( 3 x – 1 ) ( 7 x – 10 ) .
Lời giải:
a ) 2×3 + 6×2 = x2 + 3 x
⇔ ( 2×3 + 6×2 ) – ( x2 + 3 x ) = 0
⇔ 2×2 ( x + 3 ) – x ( x + 3 ) = 0
⇔ x ( x + 3 ) ( 2 x – 1 ) = 0
( Nhân tử chung là x ( x + 3 ) )
⇔ x = 0 hoặc x + 3 = 0 hoặc 2 x – 1 = 0
+ x + 3 = 0 ⇔ x = – 3 .
+ 2 x – 1 = 0 ⇔ 2 x = 1 ⇔ x = 1/2 .
Vậy tập nghiệm của phương trình là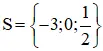
b ) ( 3 x – 1 ) ( x2 + 2 ) = ( 3 x – 1 ) ( 7 x – 10 )
⇔ ( 3 x – 1 ) ( x2 + 2 ) – ( 3 x – 1 ) ( 7 x – 10 )
⇔ ( 3 x – 1 ) ( x2 + 2 – 7 x + 10 ) = 0
⇔ ( 3 x – 1 ) ( x2 – 7 x + 12 ) = 0
⇔ ( 3 x – 1 ) ( x2 – 4 x – 3 x + 12 ) = 0
⇔ ( 3 x – 1 ) [ x ( x – 4 ) – 3 ( x – 4 ) ] = 0
⇔ ( 3 x – 1 ) ( x – 3 ) ( x – 4 ) = 0
⇔ 3 x – 1 = 0 hoặc x – 3 = 0 hoặc x – 4 = 0
+ 3 x – 1 = 0 ⇔ 3 x = 1 ⇔ x = 1/3 .
+ x – 3 = 0 ⇔ x = 3 .
+ x – 4 = 0 ⇔ x = 4 .
Vậy phương trình có tập nghiệm là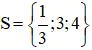

Bài 4: Phương trình tích

Luyện tập (trang 17 sgk Toán 8 Tập 2)

Bài 26 (trang 17-18-19 SGK Toán 8 tập 2): TRÒ CHƠI (chạy tiếp sức)

Chuẩn bị:
Giáo viên chia lớp thành n nhóm, mỗi nhóm gồm 4 em sao cho các nhóm đều có em học giỏi, học khá, học trung bình … Mỗi nhóm tự đặt cho nhóm mình một cái tên, ví dụ điển hình, nhóm “ Con Nhím ”, nhóm “ Ốc Nhồi ”, nhóm “ Đoàn Kết ” … Trong mỗi nhóm, học viên tự đánh số từ 1 đến 4. Như vậy sẽ có n học viên số 1, n học viên số 2, …
Giáo viên chuẩn bị sẵn sàng 4 đề toán về giải phương trình, đánh số từ 1 đến 4. Mỗi đề toán được photocopy thành n bản và cho mỗi bản vào một phong bì riêng. Như vậy sẽ có n bì chứa đề toán số 1, m bì chứa đề toán số 2 … Các đề toán được chọn theo công thức sau :
Đề số 1 chứa x ; đề số 2 chứa x và y ; đề số 3 chứa y và z ; đề số 4 chứa z và t ( xem bộ đề mẫu dưới đây ) .

Cách chơi:
Tổ chức mỗi nhóm học viên ngồi theo hàng dọc, hàng ngang, hay vòng tròn quanh một cái bàn, tùy điều kiện kèm theo riêng của lớp .
Giáo viên phát đề số 1 cho học viên số 1 của các nhóm, đề số 2 cho học viên số 2, …
Khi có tín hiệu lệnh, học viên số 1 của các nhóm nhanh gọn mở đề số 1, giải rồi chuyển giá trị x tìm được cho bạn số 2 của nhóm mình. Khi nhận được giá trị x đó, học viên số 2 mới được phép mở đề, thay giá trị của x vào, giải phương trình để tìm y rồi chuyển đáp số cho bạn số 3 của nhóm mình. Học sinh số 3 cũng làm tương tự như. học viên số 4 chuyển gái trị tìm được của t cho giáo viên ( đồng thời là giám khảo ) .
Nhóm nào nộp tác dụng đúng tiên phong thì thắng cuộc .
Lời giải:
– Học sinh 1 : ( Đề số 1 ) Giải phương trình : 2 ( x – 2 ) + 1 = x – 1 .
⇔ 2 x – 4 + 1 = x – 1
⇔ 2 x – x = – 1 + 4 – 1
⇔ x = 2 .
– Học sinh 2 : ( Đề số 2 ) Thay x = 2 vào phương trình ta được phương trình mới :
( 2 + 3 ). y = 2 + y
⇔ 5 y = 2 + y
⇔ 4 y = 2
⇔ y = 1/2

– Học sinh 3 : ( Đề số 3 ) Thay y = 1/2 vào phương trình ta được phương trình mới :

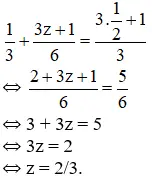
⇔ 3 + 3 z = 5
⇔ 3 z = 2
⇔ z = 2/3 .
– Học sinh 4 : ( đề số 4 ) thay z = 2/3 vào phương trình ta được :

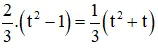
⇔ 2 ( t2 – 1 ) = t2 + t
⇔ 2 ( t2 – 1 ) – ( t2 + t ) = 0
⇔ 2 ( t – 1 ) ( t + 1 ) – t ( t + 1 ) = 0
⇔ ( t + 1 ) ( 2 t – 2 – t ) = 0
⇔ ( t + 1 ) ( t – 2 ) = 0
⇔ t + 1 = 0 hoặc t – 2 = 0
+ t + 1 = 0 ⇔ t = – 1 ( loại vì có điều kiện kèm theo t > 0 ) .
+ t – 2 = 0 ⇔ t = 2 ( thỏa mãn nhu cầu ) .
Vậy t = 2 .
Bài 4: Phương trình tích

Luyện tập (trang 17 sgk Toán 8 Tập 2)

Bài 26 (trang 17-18-19 SGK Toán 8 tập 2): TRÒ CHƠI (chạy tiếp sức)

Chuẩn bị:
Giáo viên chia lớp thành n nhóm, mỗi nhóm gồm 4 em sao cho các nhóm đều có em học giỏi, học khá, học trung bình … Mỗi nhóm tự đặt cho nhóm mình một cái tên, ví dụ điển hình, nhóm “ Con Nhím ”, nhóm “ Ốc Nhồi ”, nhóm “ Đoàn Kết ” … Trong mỗi nhóm, học viên tự đánh số từ 1 đến 4. Như vậy sẽ có n học viên số 1, n học viên số 2, …
Giáo viên sẵn sàng chuẩn bị 4 đề toán về giải phương trình, đánh số từ 1 đến 4. Mỗi đề toán được photocopy thành n bản và cho mỗi bản vào một phong bì riêng. Như vậy sẽ có n bì chứa đề toán số 1, m bì chứa đề toán số 2 … Các đề toán được chọn theo công thức sau :
Đề số 1 chứa x ; đề số 2 chứa x và y ; đề số 3 chứa y và z ; đề số 4 chứa z và t ( xem bộ đề mẫu dưới đây ) .

Cách chơi:
Tổ chức mỗi nhóm học viên ngồi theo hàng dọc, hàng ngang, hay vòng tròn quanh một cái bàn, tùy điều kiện kèm theo riêng của lớp .
Giáo viên phát đề số 1 cho học viên số 1 của các nhóm, đề số 2 cho học viên số 2, …
Khi có tín hiệu lệnh, học viên số 1 của các nhóm nhanh gọn mở đề số 1, giải rồi chuyển giá trị x tìm được cho bạn số 2 của nhóm mình. Khi nhận được giá trị x đó, học viên số 2 mới được phép mở đề, thay giá trị của x vào, giải phương trình để tìm y rồi chuyển đáp số cho bạn số 3 của nhóm mình. Học sinh số 3 cũng làm tựa như. học viên số 4 chuyển gái trị tìm được của t cho giáo viên ( đồng thời là giám khảo ) .
Nhóm nào nộp tác dụng đúng tiên phong thì thắng cuộc .
Lời giải:
– Học sinh 1 : ( Đề số 1 ) Giải phương trình : 2 ( x – 2 ) + 1 = x – 1 .
⇔ 2 x – 4 + 1 = x – 1
⇔ 2 x – x = – 1 + 4 – 1
⇔ x = 2 .
– Học sinh 2 : ( Đề số 2 ) Thay x = 2 vào phương trình ta được phương trình mới :
( 2 + 3 ). y = 2 + y
⇔ 5 y = 2 + y
⇔ 4 y = 2
⇔ y = 1/2
– Học sinh 3 : ( Đề số 3 ) Thay y = 1/2 vào phương trình ta được phương trình mới :

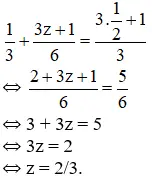
⇔ 3 + 3 z = 5
⇔ 3 z = 2
⇔ z = 2/3 .
– Học sinh 4 : ( đề số 4 ) thay z = 2/3 vào phương trình ta được :

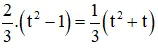
⇔ 2 ( t2 – 1 ) = t2 + t
⇔ 2 ( t2 – 1 ) – ( t2 + t ) = 0
⇔ 2 ( t – 1 ) ( t + 1 ) – t ( t + 1 ) = 0

⇔ ( t + 1 ) ( 2 t – 2 – t ) = 0
⇔ ( t + 1 ) ( t – 2 ) = 0
⇔ t + 1 = 0 hoặc t – 2 = 0
+ t + 1 = 0 ⇔ t = – 1 ( loại vì có điều kiện kèm theo t > 0 ) .
+ t – 2 = 0 ⇔ t = 2 ( thỏa mãn nhu cầu ) .
Vậy t = 2 .
Bài 4: Phương trình tích

Luyện tập (trang 17 sgk Toán 8 Tập 2)

Bài 26 (trang 17-18-19 SGK Toán 8 tập 2): TRÒ CHƠI (chạy tiếp sức)

Chuẩn bị:
Giáo viên chia lớp thành n nhóm, mỗi nhóm gồm 4 em sao cho các nhóm đều có em học giỏi, học khá, học trung bình … Mỗi nhóm tự đặt cho nhóm mình một cái tên, ví dụ điển hình, nhóm “ Con Nhím ”, nhóm “ Ốc Nhồi ”, nhóm “ Đoàn Kết ” … Trong mỗi nhóm, học viên tự đánh số từ 1 đến 4. Như vậy sẽ có n học viên số 1, n học viên số 2, …
Giáo viên sẵn sàng chuẩn bị 4 đề toán về giải phương trình, đánh số từ 1 đến 4. Mỗi đề toán được photocopy thành n bản và cho mỗi bản vào một phong bì riêng. Như vậy sẽ có n bì chứa đề toán số 1, m bì chứa đề toán số 2 … Các đề toán được chọn theo công thức sau :
Đề số 1 chứa x ; đề số 2 chứa x và y ; đề số 3 chứa y và z ; đề số 4 chứa z và t ( xem bộ đề mẫu dưới đây ) .

Cách chơi:
Tổ chức mỗi nhóm học viên ngồi theo hàng dọc, hàng ngang, hay vòng tròn quanh một cái bàn, tùy điều kiện kèm theo riêng của lớp .
Giáo viên phát đề số 1 cho học viên số 1 của các nhóm, đề số 2 cho học viên số 2, …
Khi có tín hiệu lệnh, học viên số 1 của các nhóm nhanh gọn mở đề số 1, giải rồi chuyển giá trị x tìm được cho bạn số 2 của nhóm mình. Khi nhận được giá trị x đó, học viên số 2 mới được phép mở đề, thay giá trị của x vào, giải phương trình để tìm y rồi chuyển đáp số cho bạn số 3 của nhóm mình. Học sinh số 3 cũng làm tựa như. học viên số 4 chuyển gái trị tìm được của t cho giáo viên ( đồng thời là giám khảo ) .
Nhóm nào nộp hiệu quả đúng tiên phong thì thắng cuộc .
Lời giải:
– Học sinh 1 : ( Đề số 1 ) Giải phương trình : 2 ( x – 2 ) + 1 = x – 1 .
⇔ 2 x – 4 + 1 = x – 1
⇔ 2 x – x = – 1 + 4 – 1
⇔ x = 2 .
– Học sinh 2 : ( Đề số 2 ) Thay x = 2 vào phương trình ta được phương trình mới :
( 2 + 3 ). y = 2 + y
⇔ 5 y = 2 + y
⇔ 4 y = 2
⇔ y = 1/2
– Học sinh 3 : ( Đề số 3 ) Thay y = 1/2 vào phương trình ta được phương trình mới :

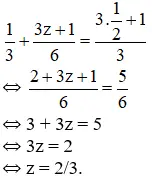
⇔ 3 + 3 z = 5
⇔ 3 z = 2
⇔ z = 2/3 .
– Học sinh 4 : ( đề số 4 ) thay z = 2/3 vào phương trình ta được :

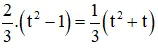
⇔ 2 ( t2 – 1 ) = t2 + t
⇔ 2 ( t2 – 1 ) – ( t2 + t ) = 0
⇔ 2 ( t – 1 ) ( t + 1 ) – t ( t + 1 ) = 0
⇔ ( t + 1 ) ( 2 t – 2 – t ) = 0
⇔ ( t + 1 ) ( t – 2 ) = 0
⇔ t + 1 = 0 hoặc t – 2 = 0
+ t + 1 = 0 ⇔ t = -1 (loại vì có điều kiện t > 0).

+ t – 2 = 0 ⇔ t = 2 ( thỏa mãn nhu cầu ) .
Vậy t = 2 .

Source: https://vietsofa.vn
Category : Góc học tập