Giải phương trình bậc nhất bằng máy tính Casio fx-580VN X

Tính năng SOLVE trong máy tính Casio fx-580VN X được cho phép tất cả chúng ta dò tìm nghiệm của phương trình bất kỳ
Tuy nhiên do những hạn chế của tính năng này mà với mỗi loại phương trình ( phương trình bậc nhất, phương trình quy về phương trình bậc nhất, phương trình tích, … ) sẽ dò theo một thuật giải riêng
Chúng ta cần làm như vậy để khai thác tối đa sức mạnh của tính năng này

Ngay bây giờ mình sẽ hướng dẫn các bạn sử dụng tính năng SOLVE hỗ trợ tìm nghiệm của phương trình bậc nhất và phương trình quy về phương trình bậc nhất

1 Nhắc lại định nghĩa

Thuật giải trình diễn bên dưới chỉ giải được phương trình bậc nhất và phương trình quy về phương trình bậc nhất
Vì vậy trước khi vận dụng bạn cần xác lập phương trình đã cho có đúng hai loại này hay không bạn nhá

1.1 Phương trình bậc nhất

Phương trình dạng với , là hai số đã cho và được gọi là phương trình bậc nhất

1.2 Phương trình quy về phương trình bậc nhất

Phương trình quy về phương trình bậc nhất chỉ các phương trình mà hai về của chúng là hai biểu thức hữu tỉ của ẩn, không chứa ẩn ở mẫu và có thể đưa về dạng

2 Thuật giải

Bước 1 Nhập phương trình vào máy tính

• Nhấn phím x hoặc nhấn phím ALPHA rồi nhấn phím ( để nhập biến
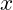
• Nhấn phím ALPHA rồi nhấn phím CALC để nhập dấu =

Bước 2 Nhấn phím SOLVE (nhấn phím SHIFT rồi nhấn phím CALC để nhấn phím SOLVE)

Bước 3 Nhập giá trị ban đầu, mình thường nhập

Bước 4 Nhấn phím =

Bước 5 Nhấn phím =

3 Hệ thống ví dụ minh họa

Ví dụ 3.1

Giải phương trình

Bước 1 Nhập phương trình vào máy tính

Bước 2 Nhấn phím SOLVE

Bước 3 Nhập giá trị bắt đầu, ở đây mình sẽ nhập

Bước 4 Nhấn phím =

Bước 5 Nhấn phím =

Vậy phương trình đã cho có một nghiệm duy nhất là

Ví dụ 3.2

Giải phương trình

Vậy phương trình đã cho có một nghiệm duy nhất là

Ví dụ 3.3

Giải phương trình

Nghiệm tìm được là một số thập phân vô hạn tuần hoàn. Để chuyển số này sang dạng thức phân số chúng ta nhấn phím Ans rồi nhấn phím =

Vậy phương trình đã cho có một nghiệm duy nhất là

Ví dụ 3.4

Giải phương trình

• 
• 

Thông báo Cannot Solve xuất hiện trên màn hình chứng tỏ không dò được nghiệm

Vậy phương trình đã cho vô nghiệm
Ví dụ 3.5

Giải phương trình

Vậy phương trình đã cho có một nghiệm duy nhất là

Kết luận trên là sai hoàn toàn vì phương trình đã cho có vô số nghiệm. Thật vậy

Chú ý

Một số phương trình quy về phương trình bậc nhất hoàn toàn có thể rơi vào trường hợp đặc biệt quan trọng là vô số nghiệm
Vì vậy khi dò được nghiệm bằng tất cả chúng ta nên dò lại một lần nữa với giá trị khởi đầu là một giá trị khác

• Nếu nghiệm tìm được vẫn là thì phương trình đã có nghiệm duy nhất là
• Nếu nghiệm tìm được là một số khác thì phương trình đã cho có vô số nghiệm

Hãy chia sẽ nếu thấy hữu dụng …

Source: https://vietsofa.vn
Category : Góc học tập