Nội dung hướng dẫn giải Bài 9: Giải toán bằng cách lập phương trình bậc hai một ẩn được chúng tôi biên soạn bám sát bộ sách giáo khoa môn Toán chương trình mới (VNEN). Là tài liệu tham khảo hữu ích giúp các em học tốt môn Toán lớp 9.
A.B. Hoạt động khởi động và hình thành kiến thức – Bài 9: Giải toán bằng cách lập phương trình bậc hai một ẩn
1. Thực hiện các hoạt động sau
Anh Hoàng chở hàng bằng xe đạp điện lên thị xã để bán. Lúc về, anh đã tăng tốc độ thêm 3 km, do đó thời hạn về ít hơn thời hạn đi là 30 phút. Tính tốc độ của anh Hoàng lúc đi, biết quãng đường từ nhà anh đến thi xã dài 30 km.
Phân tích bài toán: Đối tượng tham gia vào bài toán là anh Hoàng, các đại lượng liên quan là vận tốc (chưa biết), thời gian đi (chưa biết) và quãng đường (đã biết) theo dự định và trên thực tế. Các đại lượng quan hệ với nhau theo công thức:
Quãng đường ( km ) = Vận tốc ( km / h ) x Thời gian ( h ) Nếu chọn một đại lượng chưa biết, chẳng hạn vận tốc của anh Hoàng lúc đi là x ( km / h, x > 0 ), ta hoàn toàn có thể trình diễn các đại lượng trong bài toán như bảng dưới đây. – Điền vào ô trống trong bảng sau các số hoặc biểu thức để giải bài toán :

– Viết tiếp vào chỗ chấm ( … ) cho đúng : Hiệu giữa thời hạn đi và thời hạn về là : … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … …
Vì thời gian về ít hơn thời gian đi là 30 phút hay 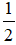
… … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … – Viết tiếp vào chỗ chấm ( … ) cho đúng : Gọi tốc độ lúc đi của anh Hoàng là x ( km / h, x > 0 ) Thời gian anh Hoàng đi từ nhà lên thị xã là : … … … … … … … … … … … … … Vận tốc lúc về của anh Hoàng là : … … … … … … … … … … … … … … … … …. Theo bài ra, thời hạn về ít hơn thời hạn đi là 30 phút hay giờ nên ta có phương trình : … … … … … … … … … … … … … … … … Giải phương trình ta được : … … … … … … … … … … … … … … … … … … … … … … Kiểm tra với điều kiện kèm theo của ẩn, ta có : … … … … … … … … … … … … … … … … … … Vậy tốc độ của anh Hoàng lúc đi là : … … … … … … … … … … … … … … … … … …
Trả lời:

• Viết tiếp vào chỗ chấm ( … ) cho đúng :
Hiệu giữa thời gian đi và thời gian về là: 
Vì thời gian về ít hơn thời gian đi là 30 phút hay giờ nên ta có phương trình: 
• Viết tiếp vào chỗ chấm ( … ) để hoàn thành xong giải thuật bài toán : Gọi tốc độ lúc đi của anh Hoàng là x ( km / h, x > 0 ).
Thời gian anh Hoàng đi từ ngày lên thị xã là: ![]()
Vận tốc lúc về của anh Hoàng là : x + 3 ( km / h )
Thời gian anh Hoàng quay trở về là: ![]()
Theo bài ra, thời hạn về ít hơn thời hạn đi là 30 phút hay giờ nên ta có phương trình :
![]()
Giải phương trình ta được: ⇔ 
Kiểm tra với điều kiện kèm theo của ẩn, ta có : x = 12 ( km / h ) Vậy tốc độ anh Hoàng lúc đi là : 12 ( km / h )
2. Đọc kĩ nội dung sau
Tóm tắt các bước giải bài toán bằng cách lập phương trình
Bước 1. Lập phương trình : + Chọn ẩn số và đạt điều kiện kèm theo thích hợp cho ẩn số ; + Biểu diễn các đại lượng chưa biết qua ẩn và các đại lượng đã biết ; + Lập phương trình biểu lộ mối quan hệ giữa các đại lượng. Bước 2. Giải phương trình. Bước 3. Trả lời. Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn nhu cầu điều kiện kèm theo của ẩn, nghiệm nào không, rồi Tóm lại.
Ví dụ. Trong một thư viện có hai máy in A và B. Để in 60 trang giấy thì máy B in lâu hơn máy A là 2 phút. Khi cùng in thì trong 1 phút cả hai máy in được tổng cộng 144 trang giấy.
a ) Tính thời hạn để máy A in được 60 trang giấy. b ) Máy B mất bao nhiêu thời hạn để in được 144 trang giấy ? Phân tích bài toán. Đối tượng tham gia vào bài toán là hai máy in A và B, các đại lượng tương quan là hiệu suất của mỗi máy in ( chưa biết ). Thời gian in của mỗi máy ( chưa biết ) và tổng số trang giấy in ( đã biết ). Các đại lượng quan hệ với nhau theo công thức : Tổng số trang giấy ( trang ) = Công suất ( trang / phút ) x Thời gian in ( phút ) Nếu chọn một đại lượng chưa biết, ví dụ điển hình thời hạn in được 60 trang giấy của máy A là x, ta hoàn toàn có thể lập bảng để trình diễn các đại lượng trong bài toán như sau :

Trong một phút, cả hai máy in được tổng số là 144 trang giấy nên :
![]() Đấy chính là phương trình cần tìm.
Đấy chính là phương trình cần tìm.
Giải. Gọi thời hạn in được 60 trang giấy của máy A là x ( phút ) ( x > 0 )
Trong một phút, máy A in được số trang giấy là: ![]()
Thời gian in được 60 trang giấy của máy B là x + 2 ( phút )
Trong một phút, máy B in được số trang giấy là: ![]()
Vì trong một phút, cả hai máy in được tổng cộng 144 trang giấy nên ta có phương trình: ![]()
Giải phương trình ta được: ![]()
Đối chiếu với điều kiện kèm theo x > 0, ta loại nghiệm x2. a ) Vậy máy A in 60 trang giấy trong phút.
b) Máy B trong một phút in được số trang là: 
Thời gian để máy B in được 144 trang giấy là : 144 : 24 = 6 ( phút )
3. Giải các bài toán sau
a ) Tìm hai số biết hiệu của chúng là 3 và tổng các bình phương của chúng là 369. b ) Một phòng họp có 70 người dự họp được sắp xếp ngồi đều trên các dãy ghế. Nếu bớt đi 2 dãy ghế thì mỗi dãy ghế còn lại phải xếp thêm 4 người mới đủ chỗ ngồi. Hỏi lúc đầu phòng họp có mấy dãy ghế và mõi dãy ghế xếp được bao nhiêu người ?
Trả lời:
a ) Gọi số bé là a ; số lớn là a + 3 Theo bài ra, tổng bình phương của chúng là 369, nên ta có phương trình : a2 + ( a + 3 ) 2 = 369 ⇔ 2 a2 + 6 a – 360 = 0 ⇔ a2 + 3 a – 180 = 0
Giải phương trình trên ta được: 
TH1: Số bé là 12, số lớn là 15
TH2 : Số bé là – 15 ; số lớn là – 12. b ) Gọi số dãy ghế bắt đầu của phòng họp là x ( dãy ghế ), ( x > 2 )
Ban đầu, số người trên mỗi dãy ghế là: ![]()
Số dãy ghế còn lại sau khi bớt đi 2 dãy ghế là : x − 2 ( dãy ghế )
Số người trên mỗi dãy ghế sau đi bớt đi 2 dãy ghế là: ![]()
Theo bài ra, khi bớt đi hai dãy ghế, thì mỗi dãy ghế phải xếp thêm 4 người mới đủ chỗ ngồi, nên ta có phương trình sau :

Giải phương trình trên ta được: 
Kết hợp với điều kiện kèm theo bài toán, số dãy ghế khởi đầu là 7 dãy và số người trong một dãy là 10 người.
C. Hoạt động luyện tập – Bài 9: Giải toán bằng cách lập phương trình bậc hai một ẩn
Câu 1: (trang 61 SGK VNEN Toán lớp 9 tập 2 chương 4)
Hai cạnh của một mảnh đất hình chữ nhật hơn kém nhau 10 m. Tính chu vi mảnh đất ấy, biết diện tích quy hoạnh của nó là 1200 mét vuông.
Bài làm:
Gọi chiều rộng mảnh đất là x ( m ) ( x > 0 ) ⇒ Chiều dài mảnh đất là : x + 10 ( m ) Theo bài ra, diện tích quy hoạnh mảnh đất là : x ( x + 10 ) = 1200 ⇔ x2 + 10 x − 1200 = 0
Giải phương trình trên, ta được: 
Kết hợp với điều kiện kèm theo, chiều rộng hình mảnh đất là 30 m, chiều dài mảnh đất là 40 m. Chu vi mảnh đất là : 2 × ( 40 + 30 ) = 140 m.
Câu 2: (trang 61 SGK Toán 9 VNEN tập 2 chương 4)
Một xe hơi hoạt động đều trên cao tốc với tốc độ đã định để đi hết quãng đường 320 km trong một thời hạn đã định. Đi được một nữa quãng đường, xe nghỉ 10 phust để bơm xăng. Để đến nơi đúng giờ, xe phải tăng tốc độ thêm 4 km / h trên nửa quãng đường còn lại. Tính thời hạn xe lăn bánh trên đường.
Bài làm:
Gọi tốc độ đã định của xe hơi là x ( km / h ) ( x > 0 )
Thời gian đã định là: ![]()
Thời gian để đi hết nửa quãng đường là: ![]()
Vận tốc đi nửa quãng đường cuối là : x + 4 ( km / h )
Thời gian đi nửa quãng đường cuối là: 
Do xe hơi nghỉ 10 phút hay 16 giờ để đổ xăng nên thời hạn thực tiễn để đi hết nửa quãng đường là :

Theo bài ra, thời hạn đi của xe hơi bằng với thời hạn dự tính, nên ta có phương trình sau :

Giải phương trình trên, ta được: 
Kết hợp với điều kiện kèm theo, tốc độ của xe hơi là : 60 km / h
Thời gian xe lăn bánh trên đường là: ![]()
Câu 3: (trang 61 SGK Toán lớp 9 VNEN tập 2 chương 4)
Một đội xe xe hơi có cùng tải trọng cần chở 36 tấn hàng từ khu vực A đến khu vực B. Khi sắp mở màn khởi hành thì có thêm 3 xe hơi cùng loại nữa, nên mỗi xe chở ít hơn 1 tấn so với dự tính. Hỏi lúc đầu đội xe có bao nhiêu xe hơi ?
Bài làm:
Gọi x ( xe ) là số xe khởi đầu của đội. ( x > 0, x ∈ N ).
Ban đầu, mỗi xe cần chở số tấn hàng là: ![]()
Sau khi thêm 3 xe cùng loại, số tấn hàng mỗi xe phải chở là: ![]()
Theo bài ra, sau khi thêm 3 xe thì mỗi xe phải trở ít hơn 1 tấn hàng, nên ta có phương trình sau :
![]()
Giải phương trình trên ta được: 
Kết hợp với điều kiện kèm theo, số xe bắt đầu của đội xe là : 9 xe.
Câu 4: (trang 61 SGK Toán VNEN lớp 9 tập 2 chương 4)
Một phòng học có 1 số ít dãy ghế tổng số 40 chỗ ngồi. Do phải xếp 55 chỗ nên người ta kê thêm một dãy ghế và mỗi dãy ghế thêm 1 chỗ. Hỏi lúc đầu trong phòng có mấy dãy ghế ?
Bài làm:
Gọi số dãy ghế có trong phòng lúc đầu là x ( dãy ) ( x > 0, x ∈ N )
Mỗi dãy ghế có số chỗ ngồi là: ![]()
Theo bài ra, để có đủ 55 chỗ ngồi thì cần phải kê thêm 1 dãy ghế và mỗi dãy ghế thêm 1 chỗ nên ta có phương trình :

Kết hợp với điều kiện kèm theo, số dãy ghế có trong phòng bắt đầu là 10 dãy hoặc 4 dãy ghế.
D.E. Hoạt động vận dụng và tìm tòi mở rộng – Bài 9: Giải toán bằng cách lập phương trình bậc hai một ẩn
Câu 1: (trang 61 Toán lớp 9 SGK VNEN tập 2 chương 4)
Bác Bình vay 200 000 000 đồng của một ngân hàng nhà nước để làm kinh tế tài chính mái ấm gia đình trong thời hạn một năm. Lẽ ra cuối năm bác phải trả cả vốn lẫn lãi, xong bác đã được ngân hàng nhà nước cho lê dài thời hạn thêm một năm nữa, số lãi của năm đầu được tính gộp vào với vốn để tính lãi năm sau và lãi suất vay vẫn như cũ. Hết hai năm bác Bình phải trả toàn bộ là 242 000 000 đồng. Hỏi lãi suất vay cho vay của ngân hàng nhà nước đó là bao nhiêu Phần Trăm trong một năm ?
Bài làm:
Gọi lãi suất vay cho vay của ngân hàng nhà nước là x / năm. ( 1 > x > 0 ) Số lãi của năm tiên phong là : 200000000 x ( đồng ) Tiền gốc để tính lãi suất vay của năm thứ 2 là : 200000000 ( x + 1 ) Số tiền lãi phải trả sau năm thứ 2 là : 200000000 ( x + ) x Tổng số tiền cả vốn lẫn lãi mà bác Bình phải trả sau 2 năm là : 200000000 ( x + 1 ) x + 200000000 ( x + 1 ) = 200000000 ( x + 1 ) ( x + 1 ) = 200000000 ( x + 1 ) 2 Theo bài ra, ta có phương trình : 200000000 ( x + 1 ) 2 = 242000000 ⇔ 100×2 + 200 x − 21 = 0
Giải phương trình trên ta được: 
Kết hợp với điều kiện kèm theo ⇒ x = 0,1 Vậy, lãi suất vay cho vay của ngân hàng nhà nước là : 10 % / năm.
Câu 2: (trang 61 SGK VNEN Toán 9 tập 2 chương 4)
Một đa giác lồi có toàn bộ 170 đường chéo. Hỏi đa giác đó có bao nhiêu cạnh ?
Bài làm:
Gọi số cạnh của đa giác lồi là x ( cạnh ), ( x > 0, x ∈ N )
Công thức tính số đường chéo của một đa giác lồi có x cạnh là: ![]()
Theo giả thiết, ta có phương trình: ![]()
Giải phương trình trên ta được: 
Kết hợp với điều kiện kèm theo bài toán, vậy, đa giác đó có 20 cạnh.
Câu 3: (trang 61 SGK Toán 9 VNEN tập 2 chương 4)
Huy đố Nam tìm được một số ít mà 50% số đó trừ đi 50% đơn vị chức năng rồi lại nhân với một nửa số đó thì bằng 50% đơn vị chức năng. Nam đã tìm đúng số đó. Em có biết Nam tìm ra số nào không ?
Bài làm:
Gọi số cần tìm là x.
Theo bài ra, ta có phương trình: ![]()
Giải phương trình trên, ta được: 
Kết hợp với điều kiện kèm theo, vậy số cần tìm là :
►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Bài 9: Giải toán bằng cách lập phương trình bậc hai một ẩn VNEN Toán 9 file PDF hoàn toàn miễn phí.
Source: https://vietsofa.vn
Category : Góc học tập




+ There are no comments
Add yours