Cách giải phương trình lượng giác (có nhiều ví dụ)

Xin chào tất cả các bạn, hôm nay chúng ta sẽ cùng nhau tìm hiểu cách giải một số lớp phương trình lượng giác thường gặp nhất ha.
Trước khi đọc bài viết này thì bạn nên xem lại cách giải phương trình bậc hai và các công thức lượng giác cơ bản trước đã bạn nhé. Việc làm này rất có ích, vì hai mảng kiến thức và kỹ năng trên được sử dụng rất nhiều khi giải các phương trình lượng giác .

#1. Công thức nghiệm của các phương trình lượng giác cơ bản

• $\sin f(x) = \sin g(x) \Leftrightarrow \left[\begin{array}{l} f(x) = g(x) + k 2\pi \\ f(x) = \pi – g(x) + k 2\pi \end{array}\right.$ với $k \in Z$
• $\cos f(x) = \cos g(x) \Leftrightarrow f(x) = \pm g(x) + k 2\pi$ với $k \in Z$
• $\tan f(x) = \tan g(x) \Rightarrow f(x) = g(x) + k \pi$ với $k \in Z$
• $\cot f(x) = \cot g(x) \Rightarrow f(x) = g(x) + k \pi$ với $k \in Z$

#2. Một số chú ý

• Phương trình lượng giác nếu có nghiệm thì sẽ có vô số nghiệm.
• Trong cùng một công thức nghiệm chỉ được sử dụng một loại đơn vị góc là độ hoặc radian.
• Đơn vị mặc định của phương trình lượng giác là radian.

#3. Tìm số đo của góc khi biết giá trị lượng giác

Tìm số đo của góc khi biết giá trị lượng giác gần như là việc làm không hề thiếu khi giải phương trình lượng giác .
Có nhiều cách để tìm số đo của góc khi biết giá trị lượng giác, thường dùng nhất là tra bảng giá trị hoặc sử dụng máy tính CASIO

Ở đây mình sẽ hướng dẫn các bạn tìm số đo của góc khi biết giá trị lượng giác bằng máy tính CASIO fx-580VN X

Bước 1. Lần lượt nhấn các phím  để thiết lập đơn vị góc là radian

Bước 2. Nhập hàm số lượng giác ngược

• Nhấn 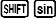để nhập hàm $\arcsin$

• Nhấn 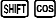để nhập hàm $\arccos$

• Nhấn 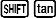để nhập hàm $\arctan$

Bước 3. Nhập giá trị lượng giác => nhấn phím  để xem số đo góc

Chú ý:
Ngay sau khi nhấn phím sẽ có hai trường hợp xảy ra:

• Trường hợp 1. Số đo góc đẹp thì sử dụng trực tiếp số đo đó luôn.
• Trường hợp 2. Số đo góc xấu thì sử dụng gián tiếp thông qua hàm “ác …”

Ví dụ. Tìm một số đo của góc $x$ thỏa mãn $\sin(x)=\frac{1}{2}$

Lần lượt nhấn các phím  để tìm số đo của góc $x$

Vậy số đo của góc USD x USD là $ \ frac { \ pi } { 6 } $
Ví dụ. Tìm một số đo của góc $x$ thỏa mãn $\cos(x)=\frac{2}{3}$

Lần lượt nhấn các phím  để tìm số đo của góc $x$

Vậy số đo của góc USD x USD là $ \ arccos \ left ( \ frac { 2 } { 3 } \ right ) USD

#4. Phương trình bậc nhất đối với một hàm số lượng giác

Phương trình bậc nhất so với một hàm số lượng giác là phương trình có dạng USD at + b = 0 USD, với $ a, b USD là các số thực, USD a $ khác USD 0 USD, USD t $ là một trong các hàm số lượng giác $ \ sin, \ cos, \ tan, \ cot USD
Các bước giải:

• Bước 1. Chuyển $b$ sang vế phải.
• Bước 2. Vì $a$ khác $0$ nên chúng ta sẽ chia hai vế của phương trình cho $a$ để đưa phương trình về phương trình lượng giác cơ bản.
• Bước 3. Giải phương trình lượng giác cơ bản.

#5. Phương trình bậc hai đối với một hàm số lượng giác

Phương trình bậc hai so với một hàm số lượng giác là phương trình có dạng USD at ^ 2 + bt + c = 0 $ với $ a, b, c USD là các số thực, USD a $ khác USD 0 USD, USD t $ là một trong các hàm số lượng giác $ \ sin, \ cos, \ tan, \ cot USD .
Các bước giải:

• Bước 1. Đặt biểu thức lượng giác bằng ẩn phụ.
• Bước 2. Đặt điều kiện cho ẩn phụ nếu có.
• Bước 3. Giải phương trình bậc hai.
• Bước 4. Tương ứng với mỗi nghiệm tìm được ở Bước 3 chúng ta sẽ giải các phương trình lượng giác cơ bản.

#6. Bài tập ví dụ

Ví dụ 1. Giải phương trình $\sin x=\frac{\sqrt{2}}{2}$

Gợi ý:
Để giải được phương trình này tiên phong bạn cần tìm được $ \ sin USD của bao nhiêu bằng $ \ frac { \ sqrt { 2 } } { 2 } $ ( tra bảng giá trị lượng giác của các góc đặc biệt quan trọng hoặc sử dụng máy tính CASIO ) .
Tiếp theo vận dụng công thức nghiệm $ \ sin f ( x ) = \ sin g ( x ) \ Leftrightarrow \ left [ \ begin { array } { l } f ( x ) = g ( x ) + k 2 \ pi \ \ f ( x ) = \ pi – g ( x ) + k 2 \ pi \ end { array } \ right. $ với USD k \ in Z $ là xong .
Lời giải:
Dễ thấy $ \ sin \ left ( \ frac { \ pi } { 4 } \ right ) = \ frac { \ sqrt { 2 } } { 2 } $
$ \ sin ( x ) = \ frac { \ sqrt { 2 } } { 2 } \ Leftrightarrow \ sin ( x ) = \ sin \ left ( \ frac { \ pi } { 4 } \ right ) \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { \ pi } { 4 } + k 2 \ pi \ \ x = \ pi – \ frac { \ pi } { 4 } + k 2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { \ pi } { 4 } + k 2 \ pi \ \ x = \ frac { 3 \ pi } { 4 } + k 2 \ pi \ end { array } \ right. $
Ví dụ 2. Giải phương trình $\cos x=\frac{2}{3}$

Gợi ý:
USD \ cos \ arccos \ left ( \ frac { 2 } { 3 } \ right ) = \ frac { 2 } { 3 } $
Áp dụng công thức nghiệm : $ \ cos f ( x ) = \ cos g ( x ) \ Leftrightarrow f ( x ) = \ pm g ( x ) + k 2 \ pi USD với USD k \ in Z USD
Lời giải

Dễ thấy $ \ cos \ arccos \ left ( \ frac { 2 } { 3 } \ right ) = \ frac { 2 } { 3 } $
USD \ cos x = \ frac { 2 } { 3 } \ Leftrightarrow \ cos x = \ cos \ arccos \ left ( \ frac { 2 } { 3 } \ right ) \ Leftrightarrow x = \ pm \ arccos \ left ( \ frac { 2 } { 3 } \ right ) + k 2 \ pi USD với USD k \ in Z USD
Ví dụ 3. Giải phương trình $\tan\left(2x+\frac{3\pi}{5}\right)=\tan\left(7x+\frac{11\pi}{13}\right)$

Gợi ý:
Áp dụng công thức nghiệm $ \ tan f ( x ) = \ tan g ( x ) \ Rightarrow f ( x ) = g ( x ) + k \ pi USD với USD k \ in Z USD
Lời giải:
USD \ tan \ left ( 2 x + \ frac { 3 \ pi } { 5 } \ right ) = \ tan \ left ( 7 x + \ frac { 11 \ pi } { 13 } \ right ) \ Rightarrow 2 x + \ frac { 3 \ pi } { 5 } = 7 x + \ frac { 11 \ pi } { 13 } + k \ pi \ Rightarrow x = – \ frac { 16 \ pi } { 325 } – k \ frac { \ pi } { 5 } $ với USD k \ in Z USD
Ví dụ 4. Giải phương trình $\sqrt{3}\tan 3x-3=0$

Gợi ý:
Phương trình này có dạng phương trình bậc nhất so với một hàm số lượng giác .
Chuyển USD – 3 $ sang vế phải rồi chia hai vế của phương trình cho $ \ sqrt { 3 } $ tất cả chúng ta sẽ được một phương trình lượng giác cơ bản .
Lời giải:
USD \ sqrt { 3 } \ tan 3 x – 3 = 0 \ Leftrightarrow \ sqrt { 3 } \ tan 3 x = 3 \ Leftrightarrow \ tan 3 x = \ frac { 3 } { \ sqrt { 3 } } $
Dễ thấy $ \ tan \ frac { \ pi } { 3 } = \ frac { 3 } { \ sqrt { 3 } } $
USD \ tan 3 x = \ frac { 3 } { \ sqrt { 3 } } \ Leftrightarrow \ tan 3 x = \ tan \ frac { \ pi } { 3 } \ Rightarrow 3 x = \ frac { \ pi } { 3 } + k \ pi \ Rightarrow x = \ frac { \ pi } { 9 } + k \ frac { \ pi } { 3 } $ với USD k \ in Z USD
Ví dụ 5. Giải phương trình $\sqrt{3}\tan^2 x-(1+\sqrt{3})\tan x+1=0$

Gợi ý:
Phương trình này có dạng phương trình bậc hai so với một hàm số lượng giác .
Đặt USD t = \ tan x USD tất cả chúng ta sẽ được phương trình bậc hai một ẩn $ \ sqrt { 3 } t ^ 2 – ( 1 + \ sqrt { 3 } ) t + 1 = 0 USD
Lời giải:
Đặt USD t = \ tan x USD
Phương trình đã cho trở thành $ \ sqrt { 3 } t ^ 2 – ( 1 + \ sqrt { 3 } ) t + 1 = 0 \ Leftrightarrow \ left [ \ begin { array } { l } t = 1 \ \ t = \ frac { \ sqrt { 3 } } { 3 } \ end { array } \ right. $

• Với $t=1$ ta được phương trình $\tan x=1 \Leftrightarrow \tan x=\tan \left(\frac{\pi}{4}\right) \Rightarrow x=\frac{\pi}{4}+k\pi$ với $k \in Z$
• Với $t=\frac{\sqrt{3}}{3}$ ta được phương trình $\tan x=\frac{\sqrt{3}}{3} \Leftrightarrow \tan x=\tan \left(\frac{\pi}{6}\right) \Rightarrow x=\frac{\pi}{6}+k\pi$ với $k \in Z$

#7. Lời kết

Okay, trên đây là cách giải phương trình lượng giác cơ bản mà bạn cần phải nắm được.
Trong trong thực tiễn tất cả chúng ta sẽ gặp nhiều phương trình lượng giác mà khi giải cần phải triển khai các phép đổi khác thích hợp để đưa chúng về các phương trình lượng giác quen thuộc
Dưới đây là 1 số ít gợi ý dành cho các bạn :

• Xem lại các công thức có liên quan đến các hàm số lượng giác như công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng ,…
• Xem thêm phương trình bậc nhất đối với $\sin x, \cos x$, phương trình thuần nhất bậc hai đối với $\sin x, \cos x$ vì đây cũng là hai dạng thường gặp.

Hi vọng bài viết này sẽ có ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Đọc thêm :
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn

Bài viết đạt : 5/5 sao – ( Có 1 lượt nhìn nhận )

Source: https://vietsofa.vn
Category : Góc học tập